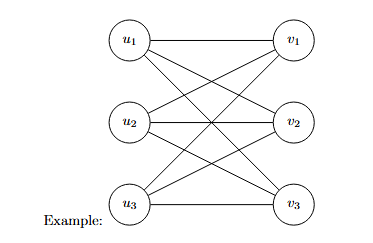
A bipartite graph is a graph whose nodes set can be partitioned into two disjoint subsets such as each edge has a node in the first subset and another in the second.
Formally that is: a bipartite graph is a graph $G=(X,Y,E)$ such that $X$, $Y$ are the two sets containing the nodes and $E$ the edge set and that:
$$\forall e \in E\text{ such as } e=(x,y) , x \in X, y \in Y \text{ and } X \cap Y = \varnothing$$
-$G$ is a $\textit{complete}$ bipartite graph if each node of $X$ is connected to each node of $Y$.
-If $|X|=|Y|$ then $G$ is called a $\textit{balanced}$ bipartite graph

A cycle in a graph is any path whose beginning node and ending node are the same.
An undirected graph is a bipartite graph if and only if it has no odd cycle.
$\textit{Proof:}$
$\Rightarrow )$ Let's suppose that $G$ is a bipartite graph containing an odd cycle $C=(v_1,\dots,v_n,v_1)$, we know that since it is an odd cycle, we can assume without loss of generality: $$\forall (v_i,v_{i+1})_{i\in [|1,n|]}\text{ with } v_{n+1}=v_1 , v_i \in X, v_{i+1} \in Y$$ but this will result in having $v_1 \in X$ and $v_{n+1}=v_1 \in Y$, yet $G$ is a bipartite graph and therefore $X \cap Y = \varnothing$ which renders our conclusion absurd, then $G$ cannot simultaneously be a bipartite graph and contains an odd cycle.
$\Leftarrow )$ Let's suppose that now $G$ if a graph containing no odd cycle. It suffices to prove the converse for connected graphs so let's consider $G$ to be a connected graph. We choose an arbitrary vertex $u$ and define a partition $(X, Y)$ of $V$ by setting $$ X =\{x \in V | d(u, x)\text{ is even}\} $$ $$ Y =\{y \in V | d(u, y)\text{ is odd}\} $$
We shall show that $(X, Y)$ is a bipartition of $G$. Suppose that $v$ and $w$ are two vertices of $X$. Let $P$ be a shortest $(u, v.)$-path and $Q$ be a shortest $(u, w)$-path. Denote by $u_1$ the last vertex common to $P$ and $Q$. Since $P$ and $Q$ are shortest paths, the $(u, u_1)$-sections of both $P$ and $Q$ are shortest $(u, u_1)$-paths and, therefore, have the same length. Now, since the lengths of both $P$ and $Q$ are even, the lengths of the $(u_1, v)$-section $P_1$ of $P$ and the $(u_1, w)$-section $Q_1$ of $Q$ must have the same parity. It follows that the $(v, w)$-path $P_1^{-1}Q_1$ is of even length. If $v$ were joined to $w$, $P_1^{-1}Q_1wv$would be a cycle of odd length, contrary to the hypothesis. Therefore no two vertices in $X$ are adjacent; similarly, no two vertices in $Y$ are adjacent.
[Bondy and Murty, 1976]
We can test whether a graph is bipartite using the depth-first search algorithm and a concept that we will develop in the future called "coloring": First of all, coloring is a procedure in which we "color" a graph by assigning a color to a node in the graph such as no adjacent nodes have the same color, we will use this principle to determine whether a graph is bipartite or not.
Basically a depth-first search of a graph rearrange the graph in a tree like fashion with the starting node being the root, if we color each node a different color from it's parent, the coloring of the resulting tree will be correct unless we have an odd cycle in which we will have two nodes at the same level of the tree having the same color and being also adjacent, so after conducting a depth-first search on the graph and coloring the nodes, all we do is check if adjacent nodes at the same level of the tree have different colors if so then there is an odd cycle and the graph isn't bipartite.
Here is an implementation of it in python:
from collections import deque
def isBipartiteDFS(adjacencyList, v):
visited = [False]*len(adjacencyList)
color = [False]*len(adjacencyList)
S=deque()
S.append(v)
#visit(v)
visited[v-1]=True
color[v-1]=True
while S:
#print(S)
v=S.pop()
for w in adjacencyList[v-1]:
if w not in S and not visited[w-1]:
S.append(w)
#visit(w)
visited[w-1]=True
color[w-1]=not color[v-1]
for node in range(len(adjacencyList)):
for neighbour in adjacencyList[node]:
if color[neighbour-1] == color[node]:
return False
return True
Note that the implementation assumes that the graph is connected
graphList = [
[2,4],
[1,3,5],
[2],
[1],
[2]
]
graphList2 = [
[3,4],
[3,6],
[1,2],
[1,5],
[4,7],
[2],
[5],
]
graphList3 = [
[2,3],
[1,3,4],
[1,2],
[2]
]
graphList4 = [
[2,4],
[1,3],
[4],
[1]
]
print("isbipartite=", isBipartiteDFS(graphList, 2))
print("isbipartite=", isBipartiteDFS(graphList2, 3))
print("isbipartite=", isBipartiteDFS(graphList3, 1))
print("isbipartite=", isBipartiteDFS(graphList4, 1))
isbipartite= True isbipartite= True isbipartite= False isbipartite= True
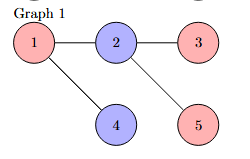
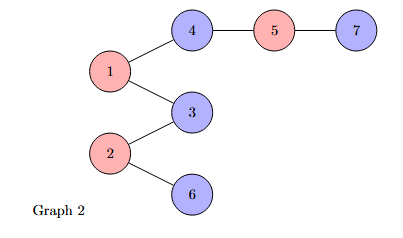
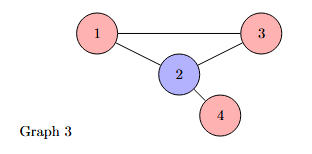
In the same spirit of the DFS algorithm, we can determine if there exists an odd cycle in a graph and therefore if it is bipartite using a breadth first search, again we use the same procedure of "coloring" the graph and check if two nodes at the same level of the resulting tree are adjacents and have the same color.
def isBipartiteBFS(adjacencyList, v):
visited = [False]*len(adjacencyList)
color = [False]*len(adjacencyList)
Q=deque()
Q.append(v)
#visit(v)
visited[v-1]=True
while Q:
v=Q.popleft()
for w in adjacencyList[v-1]:
if w not in Q and not visited[w-1]:
Q.append(w)
#visit(w)
visited[w-1]=True
color[w-1]=not color[v-1]
for node in range(len(adjacencyList)):
for neighbour in adjacencyList[node]:
if color[neighbour-1] == color[node]:
return False
return True
graphList = [
[2,4],
[1,3,5],
[2],
[1],
[2]
]
graphList2 = [
[3,4],
[3,6],
[1,2],
[1,5],
[4,7],
[2],
[5],
]
graphList3 = [
[2,3],
[1,3,4],
[1,2],
[2]
]
graphList4 = [
[2,4],
[1,3],
[4],
[1]
]
print("isbipartite=", isBipartiteBFS(graphList, 2))
print("isbipartite=", isBipartiteBFS(graphList2, 3))
print("isbipartite=", isBipartiteBFS(graphList3, 1))
print("isbipartite=", isBipartiteBFS(graphList4, 1))
isbipartite= True isbipartite= True isbipartite= False isbipartite= True
Next up is Eulerian graphs and the famous puzzle of the seven bridges of Königsberg.
[Bondy and Murty, 1976] = Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. MacMllan, London. p15